Code your GPT2 Architecture from Scratch in PyTorch!
The Generative Pre-trained Transformer (GPT) generates new text when you give prompts. We will understand and code the entire architecture from scratch using PyTorch. Are you ready to learn it?
This tutorial will not give you any philosophy, or artistic introduction. This is real stuff - real math, and real coding. If you do not understand something, you must humbly return to the basics, like I have done so many times while writing this. Take your time to learn, and come back again, and again. The Generative Pre-trained Transformer (GPT) generates new text when you give prompts. We will understand and code the entire architecture from scratch using Pytorch. In other words, you will learn how to code the function f(x), which learns the relationship between words and predicts the next word. This tutorial needs you to know the following:
Deep Learning Fundamentals
Coding Experience in PyTorch
Introduction to GPT
Linear Algebra
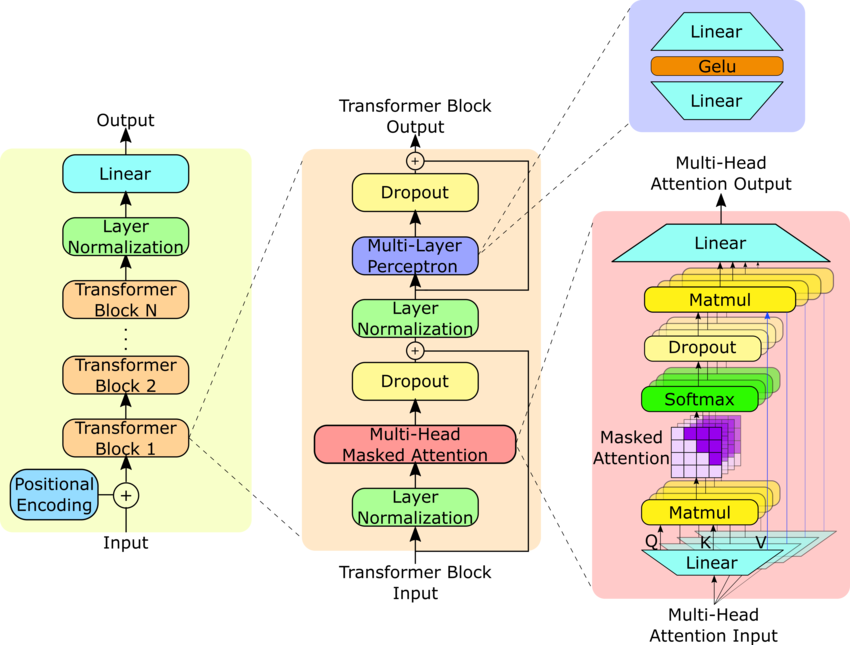
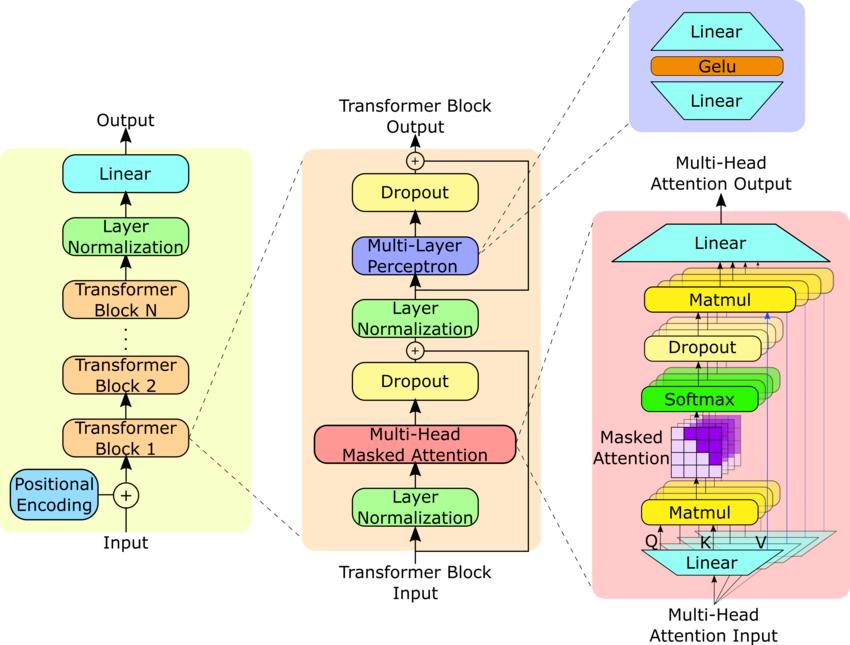
Architecture is a fancy way of artistically representing a bunch of compositions of functions which is the function f(x), you want to learn from data (text). The fun and relatively new parts are the training process, and coding the architecture. The following is the architecture of GPT2.
We will now understand what type of data, how data is fed into the network, and how the machine learns. Remember, that we will devote a large amount of our focus to understanding the dimensions of the data, and that's exactly how we will understand what's going on under the hood.
The Training Process of GPT2
This is a toy example. In the ideal case, there are lots of nuances. We will not discuss everything in detail. However, this is aimed to make it educational. The learning outcomes of this small module are to understand how is the training done, what is the input data, and what is predicted. This will help us understand the loss function, which is nothing but the cross entropy loss. But the cross-entropy loss of what? What is the input, and what is the output?
Data for Training: Text (for example the entire text of a textbook). This text is nothing but a sequence of characters, with quite a lot of patterns. If you are writing English, then, you must come after q, and the text has innumerable patterns, grammar, and a lot of representations. The goal is to create a process that learns this structure. We will assume that we will learn the relationship of the characters of a text in this entire tutorial.
Vocabulary: The set of unique characters of the entire text. In the English language, this can be written as a set of 52 characters at least - 26 capital letters, and 26 small letters, along with different punctuations. We want to assign one unique number or vector to each of these characters.
Representation: Numerical Representation of the Data. The text should be transformed into a numerical representation because a computer only understands numbers. We can do that at a very simple level. For example, one way to do this is a character-level transformation. Assign one unique number or vector to each of the unique characters.
Training and Patterns: You should learn from all possible sequences of characters X = [a1, a2, a3, a4, ..., an], and Y = [a(n+1)] from the text. From a text of size "N" characters, there are at the order of N^2 such sequences possible as X, and the corresponding next character as Y. If you have 10^6 characters in a text, it increases to 10^12. So we have to do the training in a properly optimized memory efficient way.
Context Length: The context length is therefore a way to select a sensible sequence length or context for the data to learn from - the value "n" in the previous point. It will be kept fixed in the sense that every sequence length can have a max length of "n". The model will therefore learn the context of the characters till "n" length around it. There is a small thing to say here. Understand that for a context length of n = 3 and a sequence [x1, x2, x3], we will learn the relationship between {[x1], [x2]}, {[x1, x2], [x3]}, {[x1, x2, x3], [x4]}. The notation is of the format {[x], [y]} here. Yes, you are right that there can be information loss here, but it works when trained over a longer time (empirically). If you know any mathematical paper proving why this works, please share it in the comments.
Parallel Computation: We will see that instead of just taking every sequence of the size of all possible windows less than or equal to the context length, and then computing the relationship between that sequence, it will be easier if we somehow use [x1, x2, x3] as X, and [x2, x3, x4] as Y by a clever computation to learn the relationship between {[x1], [x2]}, {[x1, x2], [x3]}, {[x1, x2, x3], [x4]} at a single go. This is called parallel computation, and it saves a lot of time and memory storage. This is a massive advantage of transformer-based architecture over the previous sequential language models.
Batch Size, Input Shape, and Training: Now, let's talk about the most important part of the training. This is important to know, and I got stuck for some time. Let's say you have a pair of input and output - the first one is {[x1], [x2]}, and the second one is {[x1, x2], [x3]}. The question is how to train them together. This is an issue when your selection for training is towards the end of the text sequence and if the context length is selected sequentially. Understand that for a context length, you will never learn the stand-alone relationship between x1 and x2, but the relationship of x2 with everything before x1. In some cases, people use padding of 0s to artificially increase the size of the list from [x1] to [0, x1]. Then, a batch size of such randomly or sequentially selected lists of size context length is selected for both input and output, and in each epoch, the loss is averaged over the prediction of xs and ys in that batch, and the gradient is used to update the parameters. Remember that x and y should be of the context length always, where y is shifted from x by a one-time point to the right.
Evaluation and Text Generation: The evaluation and text generation is done in a fun way. A prompt is nothing but a sequence of characters, which can be more than the context length. So, while training the model, we should not just restrict the model to the input size compatible with the context length, but also any general length. For every batch iteration, the input size of the model is of [B, T, D], where B is the batch size, T is the sequence length (token size/context length), and D is the dimension of the representation of each character. In this case, we will take D to be 1. The evaluation is done one token (character in this case) at a time. One character is predicted by the model given an input prompt (set of characters). Then, a new input with this added character is given an input to the model, which generates a new one. We give a token size while generating the response. Let me explain the token size to you now.
Token Size: Tokens are like the atoms of the vocabulary. They are the smallest possible elements of the vocabulary. In this case, we will consider characters. In some cases, they are words and punctuation. They are decided depending on the input text to be trained on.
Input X Size = [B, T, D], and Input Y Size = [B, T, D], where a batch size B of sequences of time length T are taken. Each element of each of the sequences is of dimension D. For each batch, and a sequence, Y is a one element right shifted version of X. In this case, we will consider D = 1.
The Architecture and Code Step-by-Step
Let me pull up the image of the architecture.
Now, the first step is to understand and seek answers to the following question about the fundamental blocks of objects.
What are the fundamental classes to make, which make up the entire model class, the GPT2 class?
First of all, I would like to extend my thanks to the authors for making such a beautiful and clear image, which will help us understand the fundamental blocks. To get some prior experience or easy tutorials for coding architectures from scratch, please refer to the UNet model, which I have dissected step by step.
From the image, you can already see a few fundamental blocks to create
Input-Output Block (Left)
Transformer Block (Middle)
Multi-Head Attention Block (Right)
Observe that there are N transformer blocks one by one in the Input-Output Block. We will one more block to consider them all together.
All Transformers' Block (N Transformer Blocks together)
Observe that in the right Multi-Head Attention Block, there are parallel computations of what they call "Self Attention", whose outputs are concatenated in the end. We want a single block to calculate that self-attention.
Single-Head Attention Block (Single Block of Multi-Head Attention)
I think that's enough. So, let's summarize the fundamental blocks we need step by step sequentially.
Single-Head Attention Block
Multi-Head Attention Block
Transformer Block
GPT Model
This is in ascending order in the sense that the earlier block makes up the next block one by one. We need to code each of the blocks from scratch and understand the dimensions of the input and output of each step of the blocks. This will be long, haha.
Single-Head Attention Block
I will not explain the intuitive philosophical meaning of Queries, Keys, and Values, because I have already explained them in my Mathematics of Transformer Video. We will just select the components and code from scratch. These are the step-by-step components of the single-head attention block:
Input [B, T, E] #E is the embedding size
Query [B, T, C] (Linear Map of Input)
Key [B, T, C] (Linear Map of Input)
Value [B, T, C] (Linear Map of Input)
Matrix Multiplication of Query and Key [B, T, T]
Normalize the Matrix [B, T, T]
Masked Matrix for Parallel Computation [B, T, T]
Softmax the Normalized [B, T, T]
Dropout [B, T, T]
Matrix Multiplication of Softmax by Value [B, T, C]
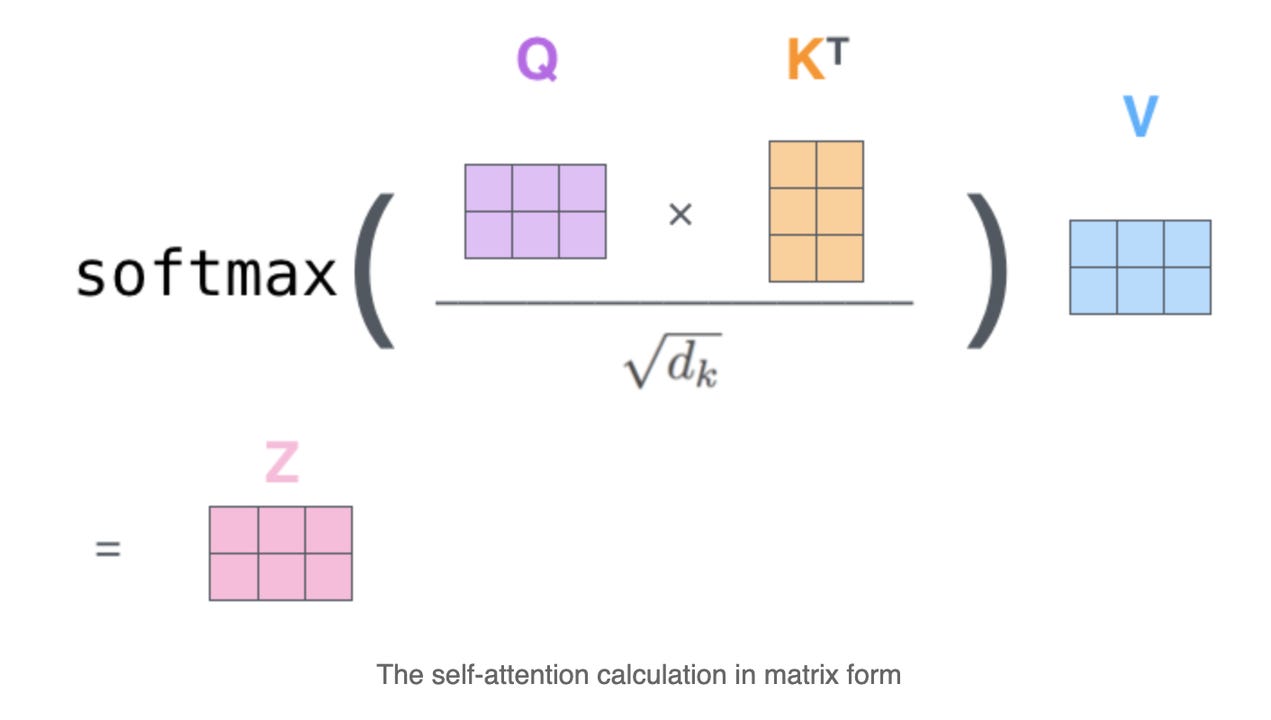
These steps are visually explained in the following image.
Let's code it. We will take an input of size [B, T, D]. The fun and interesting part is to make sure you are keeping the batch size intact, and just use the last two dimensions for multiplication. Here is how you can do it in PyTorch. Understand that while defining a class, we first select the armors (functions) of nn. modules that we need, and then in the forward portion, we will implement these step-by-step ideas. We need the input value of D, and C to the block. There is a small trick in the masking operation because we have to make sure that the mask is constant, and not updated during back propagation, but only during the forward pass in the network. The d_k here is the hidden dimension C.
Each of the steps is mentioned below in the forward function.
class Single_Head(nn.Module):
def __init__(self, inp_dim, hid_dim, drop_prob):
super(Single_Head, self).__init__()
self.hid_dim = hid_dim
self.key = nn.Linear(inp_dim, hid_dim, bias = False)
self.query = nn.Linear(inp_dim, hid_dim, bias = False)
self.value = nn.Linear(inp_dim, hid_dim, bias = False)
self.dropout = nn.Dropout(p = drop_prob)
def forward(self, x):
B, T, E = x.shape #Input [B, T, E], input_dim = E
C = self.hid_dim # hidden dimension as C
key = self.key(x) #Query [B, T, C] (Linear Map of Input)
query = self.query(x) #Key [B, T, C] (Linear Map of Input)
value = self.value(x) #Value [B, T, C] (Linear Map of Input)
matrix_mulp = query @ key.transpose(-2, -1) #Matrix Multiplication of Query and Key [B, T, T]
normalize = matrix_mulp * (C **-0.5) #Normalize the Matrix [B, T, T] with square root of C
mask = torch.ones(T, T) #create a matrix T x T of ones
mask = torch.tril(mask) #change the upper traingular part to zero
masked_matrix = normalize.masked_fill(mask == 0, float('-inf')) #Masked Matrix for Parallel Computation [B, T, T]
# this is done by takign the index of the mask where it is zero and applying the
# respective indices in the normalize matrix to be '-inf' using masked_fill function
softmax = F.softmax(masked_matrix, dim = -1) #Softmax the Normalized [B, T, T]
dropout = self.dropout(softmax) #Dropout [B, T, T]
value_update = dropout @ value #Matrix Multiplication of Softmax by Value [B, T, C]
return value_update This looks great. You can use the earlier UNet tutorial to print and understand what happens to each of the outputs' shapes. I would say this block was the most important block of the whole GPT structure.
Multi-Head Attention Block
Let's write down each of the components of the multi-head attention block. We will have several parallel attention layers, which will be concatenated. Let's write down each of the subblocks carefully. Let's assume there will be n_heads for this multi-head attention block.
n_heads number of [B, T, C] inputs
n_heads of parallel Single Attention Blocks
Concatenate n_heads outputs along the third dimension [B, T, C*n_heads] = [B, T, C']
Linear Layer [B, T, C*n_heads] = [B, T, C']
Let's call note C*n_heads as C'. This looks relatively simple. We will use a new structure called nn.ModuleList to do parallel n computations of the different attention blocks.
class Multi_Head(nn.Module):
def __init__(self, inp_dim, hid_dim, drop_prob, n_heads): #n_heads number of [B, T, C] inputs
super(Multi_Head, self).__init__()
self.hid_dim = hid_dim
self.attentionblocks = nn.ModuleList([Single_Head(inp_dim, hid_dim, drop_prob) for i in range(n_heads)]) #n_heads of parallel Single Attention Blocks
self.linear = nn.Linear(hid_dim*n_heads, hid_dim*n_heads) #Linear Layer [B, T, C]
def forward(self, x):
x = torch.cat([h(x) for h in self.attentionblocks], dim = -1) #Concatenate n_heads outputs along the third dimension [B, T, C*n_heads]
print(x.shape)
x = self.linear(x) #Linear Layer [B, T, C]
return xThis was easy. So, the right block is complete. Now, it is time to create the Transformer Block.
Transformer Block
Similar to the previous one, let's write down the components of the transformer block. The self-attention layer was the fun part. Now, all of the following will be quite easy to do, given you have understood the above. The following are the components of the transformer block. The only interesting part of the transformer block is the skip connection. We will learn something interesting from this.
Input Tensor [B, T, C]
Layer Normalization [B, T, C]
Multi-Head Attention Block [B, T, C']
Dropout [B, T, C']
Skip Connection [B, T, C']
Layer Normalization [B, T, C']
Linear Layer [B, T, 4C']
GeLu [B, T, 4C']
Linear Layer [B, T, 4C']
Dropout [B, T, C']
Skip Connection [B, T, C']
These look pretty straightforward and albeit a large list, apart from the skip connection. You can divide the linear and the GeLu layers together into a different module class, but I am doing this block together.
class Transformer_Block(nn.Module):
def __init__(self, inp_dim, hid_dim, drop_prob, n_heads):
super(Transformer_Block,self).__init__()
n_embd =
self.layer_norm1 = nn.LayerNorm(inp_dim) #Layer Normalization [B, T, C]
self.multi_head = Multi_Head(inp_dim, hid_dim, drop_prob, n_heads) #Multi-Head Attention Block [B, T, C']
self.dropout1 = nn.Dropout(drop_prob) #Dropout [B, T, C']
#skip connection here
self.layer_norm2 = nn.LayerNorm(hid_dim*n_heads) #Layer Normalization [B, T, C']
self.linear1 = nn.Linear(hid_dim*n_heads, 4*hid_dim*n_heads) #Linear Layer [B, T, 4C']
self.gelu = nn.GELU() #GeLu [B, T, 4C']
self.linear2 = nn.Linear(4*hid_dim*n_heads, hid_dim*n_heads) #Linear Layer [B, T, 4C']
self.dropout2 = nn.Dropout(drop_prob) #Dropout [B, T, C']
#skip connection here
#skip connnections will be there in the feedforward network part
def forward(self, x):
x1 = self.layer_norm1(x) #Layer Normalization [B, T, C]
x1 = self.multi_head(x1) #Multi-Head Attention Block [B, T, C']
x1 = self.dropout1(x1) #Dropout [B, T, C']
x1 = x + x1 #Skip Connection [B, T, C']
x1 = self.layer_norm2(x1) #Layer Normalization [B, T, C']
x2 = self.linear1(x1) #Linear Layer [B, T, 4C']
x2 = self.gelu(x2) #GeLu [B, T, 4C']
x2 = self.linear2(x2) #Linear Layer [B, T, 4C']
x2 = self.dropout2(x2) #Dropout [B, T, C']
x3 = x1 + x2 #Skip Connection [B, T, C']
return x3Aah! Skip connections are easy to implement. Just play of variable change. This engineering is pretty easy, fun, and interesting. We are now ready to use the three blocks to make the final GPT2 model. We must ensure that we have n_trans Transformer Blocks in the actual GPT2 model.
GPT Model
There we are finally. We will now write down the fundamental blocks to create this GPT model carefully. There is a small dimension analysis catch, that you should focus on, and you wouldn't have understood, if I had fixed the numbers at the beginning. So, please be careful and attentive here.
Input [B, T, D]
Input Embedding [B, T, E]
Positional Embedding [B, T, E]
Input + Positional Embedding Sum [B, T, E]
n_trans = Number of Transformer Blocks
This is where the catch comes in. If we input this through a transformer model, we get an output of size [B, T, C'], where we C' = n_heads*C. Again, if we input this through the n_trans number of blocks. The final C' will be huge = (n_heads^n_trans)*C. For simplicity of calculations and memory, E and C' need to be the same, so it can easily pass through the blocks. Thus E = C'. This leads to the identity that the
E (embedding size) = C (hidden or head size) * n_heads (# heads)
Please make sure, we input this while coding the GPT architecture. Okay, now time for the remaining part of the architecture.
n_trans number of Transformer Blocks [B, T, E]
Layer Normalization [B, T, E]
Linear Layer [B, T, V]
V is the size of the Vocabulary. This is because, for every time point, we are predicting the logits of each of the elements in the vocabulary, out of which we are selecting the best one. It's time for code now.
batch_size = 32 #batchsize
context_length = 8 #context_length
D = 1 #
inp_dim = 64 #embedding dimension
hid_dim = 16 #hidden dimension / head size
n_heads = 4 # number of multi attention heads
# observe that inp_dim = hid_dim * n_heads
n_trans = 4 # number of transformer blocks
drop_prob = 0.6 #dropout probability
vocab_size = len(vocabulary)
class GPT2(nn.Module):
def __init__(self, inp_dim, hid_dim, drop_prob, n_heads, n_trans, vocab_size):
super(GPT2, self).__init__()
self.embedding = nn.Embedding(vocab_size, inp_dim) #Input Embedding [B, T, E]
self.pos_embed = nn.Embedding(context_length, inp_dim) #Positional Embedding [B, T, E]
#Input + Positional Embedding Sum [B, T, E]
nn.ModuleList([Single_Head(inp_dim, hid_dim, drop_prob) for i in range(n_heads)])
self.transformer_blocks = nn.Sequential(*[Transformer_Block(inp_dim, hid_dim, drop_prob, n_heads) for i in range(n_trans)]) #n_trans number of Transformer Blocks [B, T, E]
self.layer_norm = nn.LayerNorm(inp_dim) #Layer Normalization [B, T, E]
self.linear = nn.Linear(inp_dim, vocab_size) #Linear Layer [B, T, V]
def forward(self, x):
B, T = x.shape
x1 = self.embedding(x) #Input Embedding [B, T, E]
x2 = self.pos_embed(torch.arange(T, device=device)) #Positional Embedding [T, E]
x = x1+x2 #Input + Positional Embedding Sum [B, T, E]
x = self.transformer_blocks(x) #n_trans number of Transformer Blocks [B, T, E]
x = self.layer_norm(x) #Layer Normalization [B, T, E]
x = self.linear(x) #Linear Layer [B, T, V]
return xLet's test this on fake input data, to see the output. Let's select the proper parameters of the network. However, there should be a disclaimer to do this. nn.Embedding works interestingly. It is a linear map, but it takes only takes in the input integers as indices. Based on those indices the respective linear map is done, instead of having a very large matrix, and then selecting the appropriate linear map, which can take time. Read about it here. To clarify, the input to the model are integers, which are mapped from the text data, where each token (character) is an integer, which is nothing but an index. Based on that index, the embedding is chosen just after the input to the model. Since the index value of any token cannot be larger than the vocabulary size, we have to make sure while generating a random input. Positional embedding is also generated based on the time dimension (token size/context length) because it is just interested in the position information. Both the embeddings map to the same input dimension.
batch_size = 32 #batchsize
context_length = 8 #block_size
inp_dim = 64 #embedding dimension
hid_dim = 16 #hidden dimension / head size
n_heads = 4 # number of multi attention heads
# observe that inp_dim = hid_dim * n_heads
n_trans = 4 # number of transformer blocks
drop_prob = 0.6 #dropout probability
vocab_size = len(vocabulary)Observe that the vocabulary size is important, as the random input should be generated based on the vocabulary size so that the integer inputs are the indices to the model, which the model can process to create the embeddings.
input = torch.randint(low=0, high=vocab_size, size=(batch_size, context_length))
model = GPT2(inp_dim, hid_dim, drop_prob, n_heads, n_trans, vocab_size)
model.eval()
output = model(input)
print(output.shape)You will get the output size to be the following.
torch.Size([32, 8, 91])This is perfect as we have expected since each batch's sequence of size context_length will generate a set of logits over the entire vocabulary (remember that vocabulary size = 91), and then based on that the cross entropy loss should be calculated. Huh! This was fun. Right?
This was long. Haha. I hope you will read through it, to the end step by step, and learn something interesting out of it. I firmly believe you will get immense value if you give some time to it. Feel free to ask your doubts in the comments. I would love to answer them. This took 62+ hours to create this content for you to understand. Your suggestions, feedback, and views will inspire me to make more content for your learning journey. Thank you. If you find it useful, please please show your support. Your support will help me :D Andrej Karpathy's work has been a big inspiration for me. His YouTube about section made me a big fan of Andrej. This post is my humble attempt to "pay him back". More payingback is left, though. Haha. I hope he gets to know about it. :D
The time needed to create this: 62+ hours
Follow Srijit Mukherjee for more.